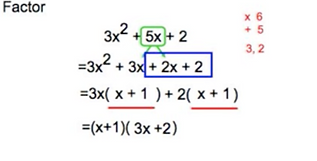Step 1

"Find The Product and sum"

Find two numbers that give the product of "c" and add up for "b" for example 3,9 give a product of 27 but also add up to 12.

Step 2

"Finally look at the signs of "b" and "c" in the givin expression to determine if the numbers are negative or positive to finalize your answer

Keep in mind of these few rules when evaluating simple or complex trinomials...

If "b" is negative and "c" is positive, both "r" and "s" are negatvie
If both "b" and "c" are positive. then both "r" and "s" are positive
If both "b" and "c" are negative or if only "c" is negative, then most likely one of "r" and "s" is negative

GCF with Trinomial Factoring

If an equation comes up where you have a greatest common factor in all the terms, then take it out of the bracket and do the above steps if there is no co-efficient with x^2. For the example on the right, GCF is "2" and leave the two outside putting brackets around your simplifyed expression " 2(x^2-11x+28). You aren't required to do so but it will make your expression alot easier.

COMPLEX

For complex factoring of trinomials, It is where "a" is squared

You do completley the same thing but instead you will factor until you have similiar expressions and your final answer would be grouping since the final answer is "3x^2+5x+2. In the end if these are supposed to be your x-intercepts, you would have to make (3x+2) into (x-2/3) as the "x" must be alone so anything that is beside the "x" must be divided with the term beside or number which was "3", and your x intercepts are (-1,0) and (-0.67,0) (round always to nearest hundredth of the decimal place), Decimal or fraction, choice is up to you.